Measurements

Measurements of all kinds are the core of good science. Like anything else good measurements lead to good science.  There are a few fundamentals which should be kept in mind when measurements are performed.

Prime Directive:  The measurement should not change the system under investigation.

Prospective:  Keep the accuracy of the measurements within the bounds of what is needed.  Five decimal places sound great but costs much more money and time than two or none if those are sufficient to address the question.

Understanding:  Be aware of the nuances of the system so that the prime directive can be followed.

A Simple Measurement to Illustrate the Points.

                Take for example a system with two resistors, a voltage source and a voltmeter (or two).

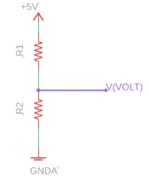
R1 = 470 K, R2= 1.00 megaohms, source = 5.000 V, and V(volt) is a very good digital voltmeter.  For conversation sake,  assume all the values assigned have great precision (0.001% tolerance).  According to Ohm’s Law the voltmeter should read 3.40 volts,  5*(R2/(R1+R2)).  The meter reads only 3.33 volts.

Trick question:  So, a second meter is connected to check the results.  The reading is even lower.  Why?

The difficulty is obvious once the details are considered.  The first is simply a violation of the prime directive.  Application of the even a good voltmeter will alter the circuit.  In this case the input impedance of this very good meter is 15 megaohms. This a respectable value for a meter but not in this case.  Connection of the meter to the circuit adds 15 megaohms in parallel to the 1.000 megaohm resistor reducing the net value to 940000.  While the 15 megaohms sounds large compared to 1.0 megaohm, the impact appears even in the first decimal place.  Understanding the circuit up front would have put the experimenter on guard.  If the resistors had been 10 times smaller the effect would not be so noticeable.

In this example, perspective is clear.  A certain value was expected and a very different value, given the simplicity of the circuit, was found.

Typically, benchtop power supplies are regulated and have very low output impedances.  No changes in the applied +5 should have occurred.

Applications of the exercise.

                If precision resistors are available, this offers a good way to measure the input impedance of a voltmeter or A to D.  Keep in mind the values of the resistors have to be high but the specific values are less important.  The author had a 1.07 megaohm resistor with 0.1% tolerance in the collection of resistors which worked well to determine the input impedance of two regularly used digital multimeters.  Going down this round will reveal that resistors with very small tolerances are very expensive.

                Keep in mind the level accuracy needed from such a measurement;  1, 10 or 20 megaohms is typically adequate.